Problemlösen durch Suchen

Voraussetzung dafür, daß ein Problem durch Suchen gelöst werden kann, ist, daß der Ausgangspunkt für die Suche, der Start, und das Ziel der Suche bekannt ist. Der Start- und Zielpunkt sind Zustände der ,,realen'' Welt. Zusätzlich müssen Aktionen bekannt sein, die ausgeführt werden können, um vom Start zum Ziel zu gelangen. Aktionen sind somit Handlungen die zu erlaubten Zwischenzuständen führen. Ziel der Suche ist es somit, eine Aktionsfolge zu finden, die vom Start zum Ziel führt. [Russell1995] 

Bei der Formulierung des Starts, des Ziels und der Aktionen muß die ,,reale'' Welt bis zu einem bestimmten Grad abstrahiert werden. Ohne diese Abstraktion würde die Komplexität des Suchproblems zu groß werden. Dies soll anhand eines Beispiels erklärt werden: Ein Vertreter will von einer Stadt zu einer anderen Stadt reisen. Denkbare Aktionen, um dieses Problem zu lösen, wären, bewege den Fuß $20cm$ nach vorne oder schlage das Lenkrad 6 Grad nach links ein, usw. Diese detailierten Einzelaktionen würden jedoch zu einem zu komplexen Suchproblem führen. Viel sinnvoller und zielführender ist es das Problem zu abstrahieren und die Aktionen als Fahrt von einer größeren Stadt zur einer anderen Stadt, mit der eine direkte Straßenverbindung besteht, zu definieren. Die reale Welt wird, zur Lösung dieses Problems, somit zu einer Straßenkarte abstrahiert. 

Zusammenfassend kann man sagen, daß das Problemlösen durch Suchen aus folgenden drei Schritten besteht: [Russell1995] 

Formulierung des Problems: 
Es werden der Start, das Ziel und die erlaubten Aktionen festgelegt. Dabei wird eine sinnvolle Abstraktion der ,,realen'' Welt vorgenommen. 
Suche: 
Es wird eine Folge von Aktionen gesucht, die vom Start zum Ziel führen. 
Ausführung: 
Es wird die Aktionsfolge, die man als Ergebnis der Suche erhalten hat, Schritt für Schritt abgearbeitet.
In den nachfolgenden Abschnitten werden nun Algorithmen zur Suche näher beleuchtet. Als Grundlage für die Erklärung dient das in Abbildung 4.1 dargestellte semantische Netz, das man auch als Graphen bezeichnen kann. Darin stellt S den Start-Node und G den Ziel-Node dar. 
\includegraphics {bilder/tech/graphennetz.eps}
Abbildung 4.1: Straßenkarte als Semantisches Netz dargestellt. Die Städte entsprechen den Nodes, die Links den Straßen und Link Labels den Kosten, die eine Benützung der Straße verursacht.
Vorstellen kann man sich den Graphen z.B. als eine Straßenkarte. Die Nodes stellen Städte dar, die Links Straßen und die Link Labels die Kosten, die eine Benützung dieser Verbindung verursacht. Erlaubte Aktionen sind somit die Fahrt auf einer Straße von einer Stadt zur nächsten. Um einen Weg vom Start-Node S zum Ziel-Node G auf dieser Straßenkarte zu finden, sind zwei Arten von Kosten zu berücksichtigen [Winston1993]: 
  1. Die Kosten, die für das Auffinden eines Lösungspfades aufgewendet werden müssen. 
  2. Die Kosten, die durch das Benutzen eines gefundenen Pfades entstehen. 
Muß man häufig von der Stadt S zur Stadt G reisen, wird man an einem möglichst kurzen und kostensparenden (optimalen) Lösungspfad interessiert sein. Um diesen zu finden, wird man auch hohe Suchkosten in Kauf nehmen. Will man jedoch nur einmal von S nach G reisen und ist es schwer den optimalen Lösungspfad mit den geringsten Kosten zu finden, wird man sich mit dem ersten gefundenen Lösungspfad zufriedengeben, auch wenn man weiß, daß es vielleicht bessere gibt. Die in Abschnitt 4.1 Blinde Suche und 4.2 Heuristische Suche vorgestellten Methoden sind in der Lage einen möglichen Lösungsweg zu finden. Suchverfahren, die den optimalen Lösungsweg finden, werden in Abschnitt 4.3 vorgestellt. 

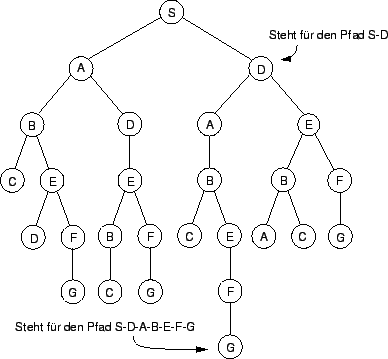
Die offensichtlichste Methode einen Weg vom Start zum Ziel zu finden, ist das Betrachten aller möglichen Wege. Wege die zu Schleifen führen, werden natürlich nicht mit berücksichtigt. Ausgehend vom Start-Node lassen sich nun alle möglichen Pfade als Baum darstellen, wie in Abbildung 4.2 gezeigt wird. Dabei ist zu beachten, daß jeder Node im Baum einen Pfad darstellt. Alle Nodes sind jedoch nur mit dem Buchstaben des Endpunktes des Pfades gekennzeichnet. [Winston1993] 

\includegraphics {bilder/tech/suchbaum.eps}
Abbildung 4.2: Der Suchbaum für das Straßenkartenproblem von Abbildung 4.1. Jeder Node bezeichnet einen Pfad, der vom Start-Node ausgeht. [Winston1993]
Eine Eigenschaft des so entstandenen Suchbaums ist der Branching-Faktor. Darunter versteht man die Anzahl der Child-Nodes $b$ die von einem Node ausgehen. Damit entspricht der Branching-Faktor der Anzahl der Nachbar-Nodes im Graphen. Ist diese Anzahl für alle Nodes im Baum gleich, so spricht man von einem Baum mit dem Branching-Faktor$b$. Der Branching-Faktor gibt somit eine Auskunft über das Wachstum des Baumes. Ein Baum mit dem Branching-Faktor $b$ besitzt in der Ebene$d$ die Anzahl von $b^{d}$ Child-Nodes. Die Ebenen werden ausgehend vom Root-Node gezählt, der sich in der Ebene 0 befindet. [Winston1993] 


4.1 Blinde Suche

Unter blinder Suche versteht man, daß zur Auffindung eines Lösungspfades keine weiteren Informationen über das Suchproblem vorliegen, die für einen effektivere Suche herangezogen werden könnten. In unserem Beispiel könnten das die Luftlinien-Entfernungen zwischen den einzelnen Städten sein. Zu den Blinden Suchen gehören die Tiefensuche, die Breitensuche und die Randomisierte Suche. [Winston1993] 

4.1.1 Tiefensuche (depth-first search)

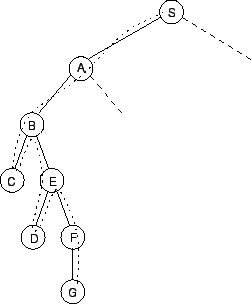
Bei der Tiefensuche wird ausgehend vom Start-Node ein Nachbar-Node besucht. Den Nachbarn des Start-Nodes im Graphen entsprechen die Children des Start-Nodes im Suchbaum. Ist dieser Nachbar noch nicht der Ziel-Node, so wird ein Nachbar dieses Nodes besucht. Dies geschieht solange, bis sich entweder eine Schleife bildet, oder der Algorithmus in eine Sackgasse gerät. In diesem Fall geht der Algorithmus soviele Schritte zurück, bis er einen Node findet, dessen Nachbarn er noch nicht alle besucht hat und setzt mit einem solchen Nachbarn fort. Abbildung 4.3 zeigt diese Vorgangsweise. Der Algorithmus ist in Abbildung 4.4 dargestellt [Winston1993]. Die Tiefensuche eignet sich damit besonders für Suchbäume, deren Äste eine vertretbare Länge nicht überschreiten. 
\includegraphics {bilder/tech/tiefensuche.eps}
Abbildung 4.3: Ein Beispiel für eine Tiefensuche. Mit jedem Schritt wird eine Ebene tiefer untersucht, bis das Ziel gefunden ist oder man an ein Blatt gelangt ist. In diesem Fall geht man den Baum soweit zurück, bis man einen Node gefunden hat, dessen Children noch nicht fertig betrachtet sind.

\begin{figure}% latex2html id marker 2043\rule{14,47cm}{0,2mm}\begin{itemi......us f\uml ur die Tiefensuche]{Algorithmus f\uml ur die Tiefensuche}\end{figure}

4.1.2 Breitensuche (breadth-first search)

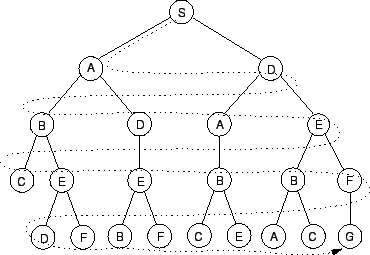
Die Breitensuche untersucht ausgehend von Start-Node alle Nachbar-Nodes. Ist der Ziel-Node noch nicht erreicht, werden alle Nachbar-Nodes der bisher untersuchten Nachbarn betrachtet, usw. Aus der Sicht des Suchbaums arbeitet man sich somit Ebene für Ebene nach unten, wie dies in Abbildung 4.5 dargestellt wird. Der Algorithmus für die Breitensuche ist in Abbildung 4.6 dargestellt. [Winston1993] 
\includegraphics {bilder/tech/breitensuche.eps}
Abbildung 4.5: Ein Beispiel für eine Breitensuche. Der Suchbaum wird Ebene für Ebene durchsucht.

\begin{figure}% latex2html id marker 2068\rule{14,47cm}{0,2mm}\begin{itemi......f\uml ur die Breitensuche.]{Algorithmus f\uml ur die Breitensuche}\end{figure}
Welcher der beiden Algorithmen verwendet werden soll, die Tiefen- oder die Beitensuche, hängt von der Aufgabenstellung ab. Die Tiefensuche eignet sich besonders für Suchbäume, deren Äste nach einer vertretbaren Anzahl von Schritten in eine Sackgasse oder zum Ziel führen. Die Tiefe des Baumes darf nicht zu groß sein. Besonders schlecht verhält sich die Tiefensuche, wenn der Suchbaum lange Äste besitzt, die nicht zum Ziel führen. 

Die Breitensuche eignet sich auch für Bäume mit großer Tiefe. Jedoch darf der Suchbaum nicht stark verzweigen. Ein großer Branching-Faktor führt zur exponentiellen Explosion der Nodes-Anzahl. [Winston1993] 

4.1.3 Nichtdeterministische Suche

Besitzt man keine Informationen über den Branching Faktor oder über die voraussichtliche Tiefe des Suchbaumes, ist es schwer, eine Entscheidung zwischen den beiden oben vorgestellten Algorithmen zu treffen. Einen Mittelweg für diesen Fall stellt die Nichtdeterministische Suche dar. Bei diesem Algorithmus wird durch Zufall bestimmt, von welchem noch nicht fertig abgearbeiteten Node, die Nachbarn untersucht werden. Der Algorithmus gleicht dem der Breiten- und Tiefensuche, jedoch werden die untersuchten Pfade an zufälliger Stelle in die Queue geschrieben. Der Algorithmus ist in Abbildung 4.7 dargestellt [Winston1993]. 

\begin{figure}% latex2html id marker 2086\rule{14,47cm}{0,2mm}\begin{itemi......che Suche.]{Algorithmus f\uml ur die Nichtdeterministische Suche.}\end{figure}


4.2 Heuristisch informierte Suche

Bei vielen Problemen lassen sich die Suchkosten dramatisch verringern, wenn man zusätzliche Informationen heranzieht, die dabei helfen, den Nachbar-Node auszuwählen, der als nächstes betrachtet werden soll. Suchverfahren die solche Informationen in ihre Suchentscheidungen einfließen lassen, heißen Heuristische4.1 Suchverfahren. 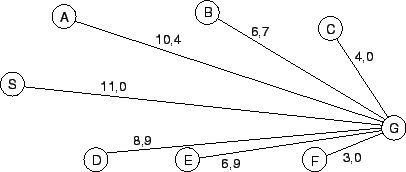In unserem Beispiel sollen als zusätzlichen Informationen die Luftlinie-Entfernung von den Nodes zum Ziel-Node herangezogen werden. Für das Straßenkarenproblem sind die Entfernungen in Abbildung 4.8 angegeben. Anhand dieser Abbildung soll das Hill-Climbing, das Beam Search und das Best-First Search Verfahren vorgestellt werden. [Winston1993] 
\includegraphics {bilder/tech/strassenluft.eps}
Abbildung: Zusätzlich zu den Informationen aus Abbildung 4.1 sind auch die Luftlinie-Entfernungen der Nodes zum Ziel-Node bekannt. Heuristische Suchverfahren verwenden diese zusätzliche Information, um die Suche effektiver zu gestalten.

4.2.1 Hill-Climbing

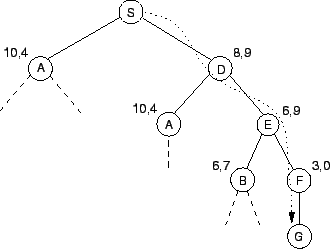
Hill-Climbing-Search verhält sich wie die Tiefensuche, mit dem Unterschied, daß zuerst der Node betrachtet wird, der die kürzeste Luftlinie-Entfernung zum Ziel hat. Abbildung 4.9 zeigt dieses Vorgehen. Bei der ersten Entscheidung liegt D näher am Ziel als A. Daher werden zuerst die Children von D untersucht. Der Algorithmus ist in Abbildung 4.10 dargestellt und gleicht dem der Tiefensuche. Es werden jedoch die Pfade sortiert, bevor sie in die Queue geschrieben werden. [Winston1993] 
\includegraphics {bilder/tech/hillclimbing.eps}
Abbildung: Der Hill-Climbing Algorithmus funktioniert wie die Tiefensuche, jedoch wird immer zuerst der scheinbar beste Pfad weiterverfolgt. Es gibt aber keine Garantie, daß der scheinbar beste Pfad auch tatsächlich der Beste ist oder überhaupt zum Ziel führt.

\begin{figure}% latex2html id marker 2123\rule{14,47cm}{0,2mm}\begin{itemi......thmus f\uml ur Hill Climbing.]{Algorithmus f\uml ur Hill Climbing}\end{figure}
Die grundsätzliche Vorgehensweise des Hill-Climbe Algorithmus und die Probleme die bei seiner Anwendung entstehen können, sollen anhand eines anderen Beispiels erklärt werden. Diese Probleme können auch bei den später vorgestellten heuristischen Suchverfahren auftreten. 

Ein Bergsteiger will einen Gipfel erklimmen. Es ist neblig. Der Bergsteiger besitzt weder eine Karte, noch befindet er sich auf einem Weg. Die einzigen Hilfsmittel die er besitzt, sind ein Kompaß und ein Höhenmesser. Um den Gipfel zu erreichen wird der Bergsteiger von seiner Position aus einen Schritt nach Norden machen, die Höhe feststellen und wieder einen Schritt zurück auf seine ursprüngliche Position gehen. Die selbe Prozedur wiederholt er für die anderen drei Himmelsrichtungen. Dies entspricht dem Untersuchen der Child-Nodes im Suchbaum. Der Bergsteiger hat nun für jede Himmelrichtung notiert, in welche Höhe er gelangen kann, wenn er einen Schritt in dieser Richtung geht und wird sich für die Richtung entscheiden, in die er die größte Höhe erreicht. Diese Vorgehensweise ist sehr effektiv. Der Bergsteiger kann jedoch auf folgenden drei Probleme stoßen. Die Bezeichnungen sind zwar an das Bergsteigen angelehnt, können aber bei allen heuristischen Suchenverfahren auftreten [Winston1993]: 

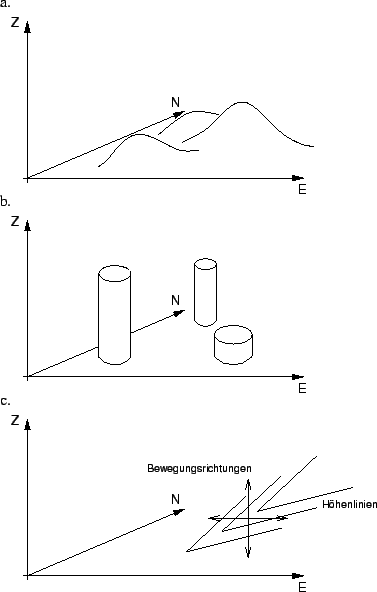
  • Vorberge: Dieses Problem tritt dann auf, wenn sich auf der Ebene, auf der sich der Bergsteiger befindet, mehrere lokale Maxima existierten, wie dies in Abbildung 4.11a dargestellt ist. Gerät der Hill-Climbe Algorithmus in die Nähe eines lokalen Maximums, so wird er von diesem angezogen. Er findet damit ein lokales Maximum, nicht aber das Ziel, ein globales Maximum. 
  • Platos: Der Bergsteiger befindet sich auf einer Ebene gleich schlechter Lösungen, weitweg von einem Maximum, das ihn anzieht. Im Extremfall sind die Maxima ganz scharfkantig ausgeprägt, wie die in Abbildung 4.11b Dargestellt ist. Der Hill-Climbe Algorithmus wird somit von keinem Maximum angezogen. 
  • Grade: Der Bergsteiger befindet sich auf dem Rücken eines Grades, der nicht in eine Richtung verläuft, in der sich der Bergsteiger bewegen kann. Da es in alle Richtungen nur bergab geht, erscheint die aktuelle Position wie ein Maximum. Eine solche Situation ist in 4.11c abgebildet. 
     

     

\includegraphics {bilder/tech/hillclimbingprob.eps}
Abbildung 4.11: Probleme, auf die man beim Hill-Climbing Algorithmus stosen kann: a. Vorberge, b. Ebene, c. Grade.
Die drei oben angeführten Probleme tragen zwar Bezeichnungen, die aus der Sprache des Bersteigens kommen, sie treten aber auch bei anderen Anwendungsgebieten auf, die mit heuristischen Suchverfahren gelöst werden sollen. Beim Beispiel mit der Straßenkarte aus Abbildung 4.1 wäre der Node C z.B. ein Vorberg. Von diesem lokalen Maximum führt keine Straße zum Ziel-Node G. 

Allgemein formuliert arbeitet der Hill-Climbe Algorithmus nach dem folgenden Prinzip: Der Algorithmus unternimmt von der aktuellen Position aus alle machbaren Schritte und mißt und bewertet wie weit ihn die einzelnen Schritte dem Ziel näher gebracht haben. Anschließend entscheidet er sich für den Schritt, der ihn scheinbar dem Ziel am nächsten bringt. Verfängt sich der Algorithmus an einem lokalen Maximum, bei dem man sich durch alle Schritte vom Ziel weg bewegt, so kann man nichtdeterministisch fortfahren. Man bewegt sich eine zufällige Anzahl von Schritten in zufällige Richtungen von der aktuellen Position fort, in der Hoffnung, dem Einzugsgebiet des lokalen Maximums zu entkommen und setzt den Hill-Climbe Algorithmus fort. Ähnlich verfährt man, wenn man sich auf einer Ebene befindet, in der Hoffnung in das Einzugsgebiet eines Maximums zu gelangen [Winston1993]. 

4.2.2 Beam Search

Beam Search verhält sich ähnlich wie die Breitensuche. Der Baum wird Ebene für Ebene abgearbeitet. Jedoch werden pro Ebene nur die w besten Pfade weiter betrachtet. Der Baum bleibt somit unabhängig vom Branching Faktor nur $w$ Pfade breit und explodiert nicht exponentiell. Abbildung 4.12 zeigt die Vorgangsweise des Beam Search Algorithmus mit $w=2$ anhand des Straßenkartenproblems. Es ist möglich, daß der Beam-Search Algorithmus keine Lösung eines Problems findet, obwohl eine Lösung existiert. Dies ist dann der Fall, wenn die $w$ scheinbar besten Pfade einer Ebene in weiterer Folge nicht zum Ziel führen. [Winston1993] 
\includegraphics {bilder/tech/beamsearch.eps}
Abbildung: Beam-Search mit $w=2$. Es werden pro Ebene im Suchbaum nur die scheinbar $w$ besten Pfade weiterverfolgt.

4.2.3 Best-First Search

Das Best-First Search Verfahren verhält sich ähnlich dem Hill-Climbing. Der Unterschied liegt im Verhalten, wenn sich ein Pfad als Sackgasse herausstellt. Das Hill-Climbing geht soviel Nodes zurück, bis es zu einen Node gelangt, von dem aus es noch nicht alle Möglichkeiten untersucht hat. Gerät das Best-First Verfahren in eine Sackgasse, so betrachtet es die Bewertungen alle Pfade, die es bereits gegangen ist und setzt den besten gefundenen, noch nicht besuchten Pfad, fort. Für das Beispiel des Straßenkartenproblems verhält sich Best-First Search und Hill-Climbing identisch, da die Suchen in keine Sackgasse gerät, wie Abbildung 4.9 zeigt. [Winston1993] 

12 Zusammenfassung

Die oben vorgestellten heuristischen Suchverfahren können nur dann eingesetzt werden, wenn sich für jeden Node eine Maßzahl bestimmen läßt, die die Entfernung zum gewünschten Suchziel widerspiegelt. Das Hill-Climbing und das Beam Search Verfahren arbeiten effektiv, wenn ein Zielpfad unter jenen Pfaden ist die bei jedem Entscheidungspunkt als die bestmöglichen erscheinen. Best-First Search arbeitet auch dann noch effektiv, wenn gute Pfade auf den ersten Blick nicht als solche erscheinen. 


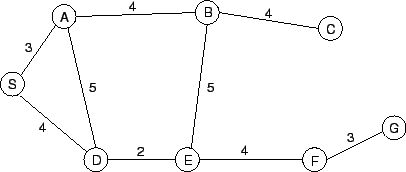
4.3 Optimale Netzsuche

In dem Graphen, der in Abbildung 4.1 dargestellt ist, sind bei den Links zwischen den Nodes Zahlen angegeben, die Link-Labels. Diese Link-Labels entsprechen den Kosten, die durch eine Benützung dieses Links entstehen. Ein optimales Suchverfahren hat nun die Aufgabe, einen Pfad von Start-Node S zum Ziel-Node G zu finden, bei dem die Summe der Kosten der benutzten Links am geringsten ist. Sieht man den Graphen aus Abbildung 4.1 als Straßenkarte an, so können die Link-Labels z.B. den Entfernungen zwischen den einzelne Städten entsprechen. Der gesuchte optimale Pfad wäre somit die kürzestmögliche Verbindung vom Start zum Ziel. In diesem Kapitel sollen nun Algorithmen vorgestellt werden, mit deren Hilfe man den optimalen Lösungspfad suchen kann. Dazu gehören die British Museum Procedure, Branch-and-Bound Search, Branch-and-Bound Search mit Abschätzung der Restkosten, Branch-and-Bound Search mit Eliminierung redundanter Doppelwege und den A$^*$ Algorithmus. 

4.3.1 British Museum Procedure

Ein mögliches Verfahren dazu ist die British Museum Procedure. Bei diesem Algorithmus werden zuerst alle möglichen Pfade von Start zum Ziel gesucht und anschließend der kürzeste daraus ausgewählt. Die Suche nach allen möglichen Lösungspfaden kann mit Hilfe der Tiefen- oder Breitensuche erfolgen, indem man den Algorithmus geringfügig ändert. Die Suchschleife soll nicht abgebrochen werden, sobald eine Lösung gefunden wurde, sondern erst nach dem für alle möglichen Pfade überprüft wurde, ob sie zum Ziel führen. Diese Methode eignet sich jedoch nur für sehr kleine Graphen. Für größere Graphen ist der Aufwand zu groß alle Pfade zu betrachten. 

4.3.2 Branch-and-Bound Search

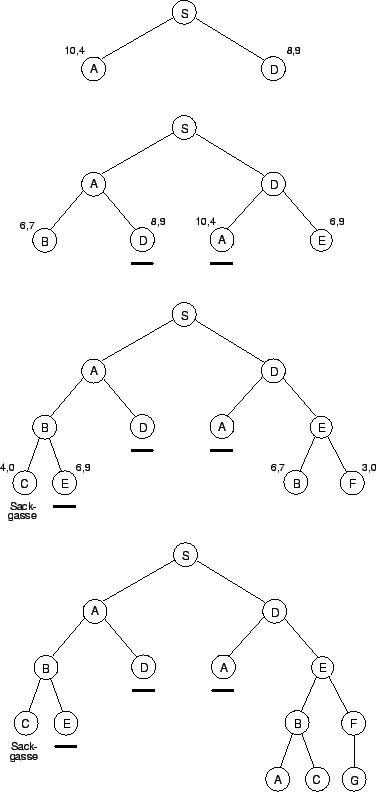
Die Idee, die hinter der Branch-and-Bound Search steht, ist folgende: Angenommen man weiß von einem Pfad, daß er vom Start zum Ziel führt und möchte überprüfen, ob es sich um den optimalen Lösungspfad handelt, so reicht es, alle anderen Pfade nur soweit zu betrachten, bis deren Kosten größer werden, als die Kosten der Benützung des optimalen Pfades. 

Die Umsetzung dieser Idee in einem Algorithmus sieht dabei wie folgt aus. Der Algorithmus erzeugt ausgehend vom Start-Node Pfade zu allen Nachbarn und berechnet die Kosten die eine Benützung des Pfades verursacht. Anschließend wird der Pfad ausgewählt, der die geringsten Kosten verursacht. Vom Endpunkt dieses Pfades aus werden nun alle Pfade erzeugt, die zu den Nachbarn dieses Nodes führen. Im nächsten Schritt werden die Kosten jedes neuen Pfades bestimmt. Aus der Menge aller Pfade wird nun der Pfad mit den geringsten Kosten ausgewählt und Pfade zu den Nachbarn des Endpunktes erzeugt. Diese Vorgehensweise wiederholt sich solange, bis ein Pfad zum Ziel-Node führt. Somit ist ein scheinbar optimaler Pfad gefunden. Um zu überprüfen, ob es sich dabei tatsächlich um den optimalen Pfad handelt, muß man alle anderen Pfade noch solange betrachten, bis deren Kosten die des scheinbar optimalen Pfades überschreiten oder mit niedereren Kosten zum Ziel führen. Überschreiten alle Pfade die Kosten des scheinbar optimalen Pfades, weiß man, daß es sich bei dem scheinbar optimalen Pfad tatsächlich um den optimalen Pfad handelt. Findet man jedoch einen Pfad, der niedrigere Kosten verursacht, so entspricht dieser dem optimalen Pfad. Der in Abbildung 4.13 dargestellte Algorithmus arbeitet besonders effektiv, wenn sich falsche Pfade schnell hohe Kosten verursachen und sie somit nicht mehr weiter berücksichtigt werden müssen. Abbildung 4.14 zeigt die Schritte beim Aufbau des Suchbaums des Straßenkartenproblems von Abbildung 4.1. [Winston1993] 


\begin{figure}% latex2html id marker 2179\rule{14,47cm}{0,2mm}\begin{itemi......d-Bound Search Algorithmus.]{Branch-and-Bound Search Algorithmus.}\end{figure}
\includegraphics [width=13.2cm]{bilder/tech/branch.eps}
Abbildung: Branch-and-Bound Search Algorithmus angewandt auf das Straßenkartenprobelem. 

4.3.3 Branch-and-Bound Search mit Abschätzung der Restkosten

Die Effizienz des Branch-and-Bound Search Algorithmus läßt sich steigern, wenn man eine Abschätzung der Restkosten als Grundlage verwendet, um zu entscheiden, welcher Pfad als nächstes um einen Schritt zu allen möglichen Nachbarn erweitert werden soll. Man sagt auch, der Pfad wird expandiert. Existiert eine gute Schätzung der Restkosten, so stellt die Summe aus den Kosten des bisher gegangenen Pfades und die geschätzten Kosten bis zum Ziel, eine gute Schätzung für die Länge des Pfades vom Start zum Ziel dar. Zum leichteren Verständnis beziehen sich die Bezeichnungen in den weiteren Erklärungen auf das Straßenkartenproblem von Abbildung 4.1. Darum wird anstelle von Kosten, von Weglängen zwischen den Städten gesprochen. Dabei darf jedoch nicht vergessen werden, daß es sich bei den Kosten auch um Zeitaufwand, um Geldeinheiten, usw. handeln kann. 

Der Algorithmus berechnet nun zu jedem Pfad die Länge des geschätzten Pfades zum Ziel und expandiert im nächsten Schritt jenen Pfad mit den geringsten geschätzten Länge. Dies geschieht solange, bis der Algorithmus beim Expandieren auf den Ziel-Node stößt. Dieser Pfad ist dann der optimale Lösungspfad, wenn die Schätzung der nachfolgenden Bedingung genügt. Die Schätzung des Restweges darf nie größer sein, als die tatsächliche Länge des Pfades zum Ziel. Wäre dies der Fall, so könnte der Suchalgorithmus dauerhaft vom optimalen Lösungspfad abgebracht werden. Dadurch kann man sich nicht mehr sicher sein, daß die Suche den optimalen Pfad als Ergebnis liefert. Unterschätzt die Schätzung den Restweg, im Extremfall mit der Länge Null, so wird dadurch lediglich die Auswahl der zunächst expandierten Pfade beeinflußt und die Effizienz sinkt, das Suchergebnis wird jedoch immer dem optimalen Pfad entsprechen. Der Algorithmus für die Branch-and-Bound Search mit Restkostenabschätzung ist in Abbildung 4.15 dargestellt. 


\begin{figure}% latex2html id marker 2201\rule{14,47cm}{0,2mm}\begin{itemi......h-and-Bound Search Algorithmus mit Absch\uml atzung der Restkosten.}\end{figure}
Für das Straßenkartenproblem stellt die Luftlinie-Entfernung zum Ziel eine gute Schätzung für den Restwert dar. Die Entfernungen sind in Abbildung 4.8 dargestellt. Es ist auch sichergestellt, daß die Schätzung nie größer ist, als die tatsächliche Entfernung zum Ziel, denn eine Straße kann nie kürzer sein, als die Luftlinie-Verbindung zwischen zwei Städten. Der schrittweise Aufbau des Suchbaumes ist in Abbildung 4.16 dargestellt. Der Branch-and-Bound Search Algorithmus mit Abschätzung der Restkosten arbeitet besonders effektiv, wenn eine gute Schätzung der Restkosten zur Verfügung steht. 
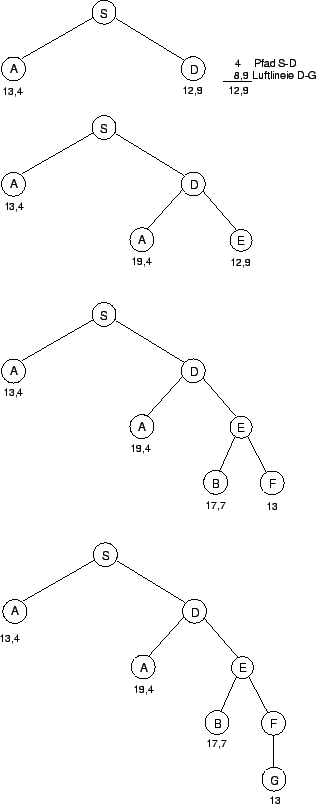\includegraphics {bilder/tech/schaetzen.eps}
Abbildung: Branch-and-Bound Search mit Abschätzung der Restkosten angewandt auf das Straßenkartenprobelem.

4.3.4 Branch-and-Bound Search mit Eliminierung längerer Doppelwege

Der Branch-and-Bound Search Algorithmus mit Eliminierung längerer Doppelwege soll anhand von Abbildung 4.17 erläutert werden. Im ersten Schritt wurde der Start-Node expandiert und die beiden Pfade A-S und S-D sind entstanden. Da der Pfad S-A kürzer ist, wird dieser zuerst weiterbetrachtet. Es entstehen die Pfade S-A-B und S-A-D. Es stellt sich nun die Frage, ob es überhaupt sinnvoll ist, den Pfad S-A-D mit der Länge 8 weiter zu betrachten, da bereits ein Pfad bekannt ist, der mit der Länge 4 zum Node D führt (S-D). Dieser Teilpfad kann somit sicher nicht zum optimalen Lösungspfad beitragen. 
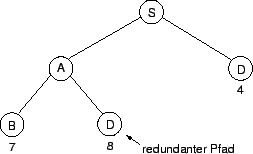\includegraphics {bilder/tech/redundant.eps}
Abbildung: Branch-and-Bound Search Algorithmus mit Eliminierung längerer Doppelwege verfolgt nur den kürzesen Pfad zu einem Node weiter.
Der Branch-and-Bound Search Algorithmus mit Eliminierung längerer Doppelwege basiert somit auf der Grundlage, daß er alle Pfade ignoriert, die zu einem Node führen, der auch durch einen anderen, kürzeren Pfad erreicht werden kann. Der Algorithmus dazu ist in Abbildung 4.18 dargestellt. Den schrittweisen Aufbau des Suchbaumes findet man in Abbildung 4.19. 

\begin{figure}% latex2html id marker 2233\rule{14,47cm}{0,2mm}\begin{itemi......ound Search Algorithmus mit Eliminierungl\uml angerer Doppelwege.}\end{figure}
\includegraphics [width=14cm]{bilder/tech/redundantstr.eps}
Abbildung: Branch-and-Bound Search Algorithmus mit Eliminierung längerer Doppelwege angewandt auf das Straßenkartenprobelem.

A$^*$ Algorithmus
 

Der A$^*$ Algorithmus stellt einen Branch-and-Bound Search Algorithmus mit Abschätzung der Restkosten und Eliminierung längerer Doppelwege dar. Die Auswahl des nächsten expandierten Pfades erfolgt über die Restwertabschätzung. Zunächst werden längere redundante Doppelwege nicht mehr weiter berücksichtigt. Bezüglich der Restwertabschätzung gilt auch die Voraussetzung, daß der Schätzwert nie größer sein darf, als der tatsächlich verbleibende Weg zum Ziel. Der Algorithmus ist in Abbildung 4.20 dargestellt. 


\begin{figure}% latex2html id marker 2256\rule{14,47cm}{0,2mm}\begin{itemi......,2mm}\caption [Der A$^*$\ Algorithmus.]{Der A$^*$\ Algorithmus.}\end{figure}

Zusammenfassung

Zusammenfassend kann man sagen, daß den British Museum Algorithmus nur für sehr kleine Suchprobleme anwendbar ist. Der Branch-and-Bound Search Algorithmus hat seine Stärken, wenn schlechte Pfade sehr schnell hohe Kosten verursachen. Ergänzt man diesen Algorithmus um die Restwertabschätzung, so steigt die Effizienz, je besser die Schätzung ist. Der Schätzwert darf jedoch nicht die tatsächlich verbleibenden Kosten zum Ziel überschreiten. Der Branch-and-Bound Search Algorithmus mit Eliminierung längerer Doppelwege arbeitet besonders effektiv, wenn viele Pfade zu einem gleichen Node führen. Der A$^*$ Algorithmus sollte dann eingesetzt werden, wenn sowohl Branch-and-Bound Search Algorithmus mit Abschätzung der Restkosten und der Branch-and-Bound Search Algorithmus mit Eliminierung längerer Doppelwege ihre Stärken aufweisen. 

Gerald Reif

2000-02-01